нами показано, что правильный выбор

Шаг 1

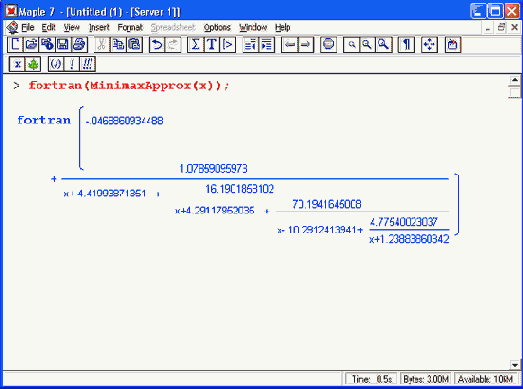
Итак, нами показано, что правильный выбор аппроксимации для сложной функции обеспечивает уменьшение времени ее вычисления более чем на два порядка (!) при весьма приличной точности в б верных знаков и при использовании для вычислений минимального числа арифметических операций. Применение при этом средств системы Maple 7 позволяет генерировать разложения в различные ряды, быстро вычислять рациональные аппроксимации функций и выполнять преобразования в различные специальные формы, сочетая это с мощными средствами интерактивной работы и графической визуализации, в частности с построением графиков функции и кривых ошибок при разных видах аппроксимации. Все это обеспечивает идеальную среду для решения таких задач.



Шаг 1

Зададим исходные числовые данные (опустив размерности):
> q:=-1.6e-19: massa:=9.1e-31: V:=le7: alpha:=80*Pi/180:
> Vx:=V*cos(alpha): Vy:=V*sin(alpha): Ex:=0:Ey:=0:Ez:=0: Bx:=0.1:By:=0: Bz:=0:
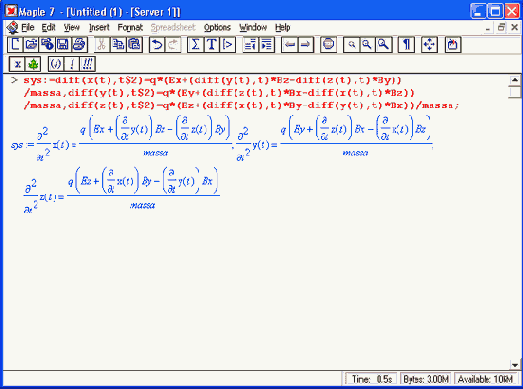
Построим траекторию движения частиц в пространстве:
> with(DEtools):DEplot3d({sys},{x(t),y(t),z(t)},t=0..2e-9, [[x(0)=O,D(x)(0)=Vx,y(0)==0,D(y)(0)=Vy,z(0)=0,D(z)(0)=0]], stepsize=le-ll,orientation=[24.117]):
Полученная траектория представлена на Рисунок 17.8. Она имеет вид спирали в пространстве. При этом скорость движения частицы вдоль оси х неизменна, а вдоль осей у и z имеет характерную колебательную компоненту. Случай явно куда менее тривиальный, чем полет камня, описанный выше.



Шаг 1



Зададим исходные числовые безразмерные данные для расчета:



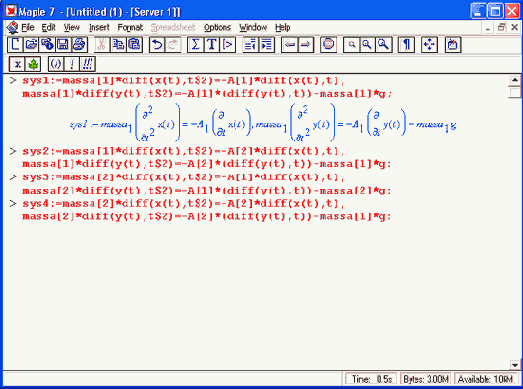
Шаг 1

Рисунок 17.9. Иллюстрация к методу разделения изотопов
В соответствии с этим дифференциальные уравнения, описывающие траекторию полета частицы по осям х, у, z имеют вид:



Шаг 1

Введем исходные числовые данные для вычислений:
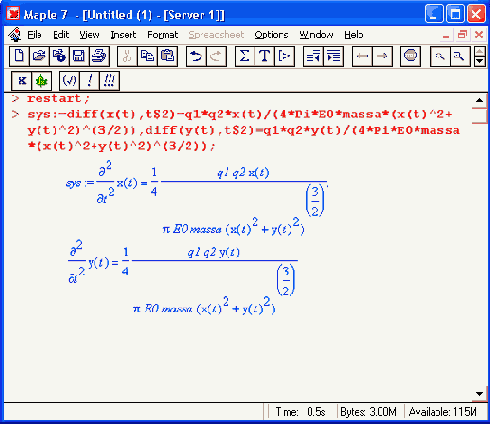
> ql:=2*i;6e-19:q2:=79*1.6e-19:massa:=4*1.67e-27:EO:=8.85e-12: a:=4e-13:
p:=5e-15:T:=4e6*1.6e-19:V0x:=sqrt(2*T/massa):
Создадим графическую структуру решения нашей системы дифференциальных уравнений для нескольких расчетных отклонений линии движения альфа- частицы от центра ядра атома, находящегося на ее пути:
> with(DEtools):ss:=DEplot({sys},{y(t),x(t)},t=0..7e-20.
[[x(0)=-a,D(x)(0)=VOx,y(0)=p,D(y)(0)=0].
[x(0)=-a,D(x)(0)=VOx,y(0)=p*4.D(y)(0)=0],
[x(0)=-a,D(x)(0)=VOx,y(0)=p*8,D(y)(0)=0],
[x(0)=-a,D(x)(0)=VOx,y(0)=p*12,D(y)(0)=0].
[x(0)=-a;D(x)(0)=VOx,y(0)=p*16,D(y)(0)=0],
[x(0)-a.D(x)(0)-VOx.y(0)-p*20,D(y)(0)-0].
[x(0)=-a,D(x)(0)=VOx,y(0)=p*24,D(y)(0)=0],
[x(0)=-a,D(x)(0)=VOx,y(0)=p*28,D(y)(0)=0]],
x(t)=-a..a,scene=[x(t),y(t)],stepsize=le-21,1inecolor=bl ack):
> with(plottools):yy:=circle([0.0],2E-14,color=red,thickness=2):
Warning, the name translate has been redefined
Построим центр ядра (кружок со знаком +) и траектории альфа- частиц:
> ss2:=PLOT(TEXT([0.-0.3e-14],'+'), FONT(HELVETICA, OBLIQUE.14)):
Осталось построить график траекторий движения альфа- частиц вблизи центра атома: i
> with(plots):
Warning, the name changecoords has been redefined
> disp1ay([ss,yy,ss2],tit1e='Pacceивание а-частиц',axes=framed);
График траекторий движения альфа- частиц вблизи ядра представлен на Рисунок 17.11. Этот график настолько нагляден, что не требует пояснения.
Моделирование движения альфа- частиц вблизи малого и «массивного» ядра атома дает наглядное представление о математической и физической сути данного опыта. Надо лишь помнить, что нельзя нацеливать альфа- частицы прямо в центр ядра. Более сложные, чем приведенные, расчеты показывают, что при этом альфа-частица настолько близко подходит к ядру, что надо учитывать новые факторы, возникающие при близком взаимодействии. Они могут привести к тому, что частица будет поглощена ядром- Но это уже тема нового разговора,, выходящего за рамки данной книги.



Шаг 1

Рисунок 17.16. Схема полосового фильтра на интегральном операционном усилителе
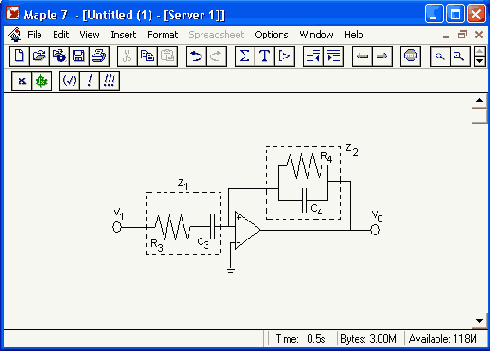
Подготовимся к расчету фильтра:
> restart:
Зададим основные уравнения, описывающие работу фильтра на малом сигнале:

Содержание раздела

---